Remarques

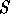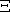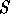1. Cette procédure ne donne pas de résultat lorsque la grammaire est ce qu'on appelle récursive à gauche (le mot récursif n'a pas ici tout à fait le même sens que dans les procédures récursives), c'est à dire lorsqu'il existe une suite de dérivations partant d'un de et conduisant à un mot qui commence par . Tel est le cas pour la première forme de la grammaire des expressions arithmétiques infixes qui ne peut donc être analysée par l'algorithme ci dessus.

2. Les transformations que l'on applique au mot s'expriment bien à l'aide d'une pile dans laquelle on place le mot à analyser, sa première lettre en sommet de pile.

3. Cette procédure est très coûteuse en temps lors de l'analyse d'un mot assez long car on effectue tous les essais successifs des règles et on peut parfois se rendre compte, après avoir pratiquement terminé l'analyse, que la première règle que l'on a appliquée n'est pas la bonne. Il faut alors tout recommencer avec une autre règle et éventuellement répéter plusieurs fois. La complexité de l'algorithme est ainsi une fonction exponentielle de la longueur du mot à analyser.

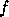4. Si on suppose qu'aucune règle ne contient un membre droit égal au mot vide, on peut diminuer la quantité de calculs effectués en débutant la procédure d'analyse par un test vérifiant si la longueur de est supérieure à celle de . Dans ce cas, la procédure d'analyse doit avoir pour résultat false. Noter que dans ces conditions la procédure d'analyse donne un résultat même dans le cas de grammaires récursives à gauche.