Les algorithmes d'analyse ascendante sont souvent plus compliqués que
ceux de l'analyse descendante. Ils s'appliquent toutefois à un beaucoup plus grand nombre
de grammaires. C'est pour cette raison qu'ils sont très souvent utilisés. Ils sont ainsi
à la base du système yacc qui sert à écrire des compilateurs sous le
système Unix. Rappelons que l'analyse ascendante consiste à retrouver la
dérivation
S0 ® u1® u2® u1 . . . un-1® un= f
en commençant par un-1 puis un-2 et ainsi de suite jusqu'à remonter à l'axiome S0. On effectue ainsi ce que l'on appelle des réductions car il s'agit de remplacer un membre droit d'une règle par le membre gauche correspondant, celui-ci est en général plus court.
Un exemple de langage qui n'admet pas d'analyse syntaxique descendante simple, mais sur lequel on peut effectuer une analyse ascendante est le langage des systèmes de parenthèses. Rappelons sa grammaire:
S ® aSbS S ® aSb S ® abS S ® ab
On voit bien que les règles S ® aSbS et S ® aSb peuvent engendrer des mots ayant un facteur gauche commun arbitrairement long, ce qui interdit tout algorithme de type LL(K). Cependant, nous allons donner un algorithme simple d'analyse ascendante d'un mot f.
Partons de f et commençons par tenter de retrouver la dernière dérivation, celle qui a donné f = un à partir d'un mot un-1. Nécessairement un-1contenait un S qui a été remplacé par ab pour donner f. L'opération inverse consiste donc à remplacer un ab par S, mais ceci ne peut pas être effectué n'importe où dans le mot, ainsi si on a
f = ababab
il y a trois remplacements possibles donnant
Sabab abSab ababS
Les deux premiers ne permettent pas de poursuivre l'analyse. En revanche, à partir du troisième, on retrouve abS et finalement S. D'une manière générale on remplace ab par S chaque fois qu'il est suivi de b ou qu'il est situé en fin de mot. Les autres règles de grammaires s'inversent aussi pour donner des règles d'analyse syntaxique. Ainsi:
On a un algorithme du même type pour l'analyse des expressions arithmétiques infixes engendrées par la grammaire:
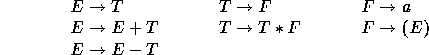
Cet algorithme tient compte pour effectuer une réduction de
la première lettre qui suit le facteur que l'on envisage de réduire (et de ce qui se
trouve à gauche de ce facteur). On dit que la grammaire est LR(1).
La théorie complète de ces grammaires mériterait un plus long développement. Nous nous
contentons de donner ici ce qu'on appelle l'automate LR(1)
qui effectue l'analyse syntaxique de la grammaire, récursive à gauche, des expressions
infixes. Noter que l'on a introduit l'opérateur de soustraction qui n'est pas associatif.
Ainsi la technique d'analyse décrite au début du paragraphe 
ne
peut être appliquée ici.
On lit le mot à analyser de gauche à droite et on effectue les réductions suivantes dès qu'elles sont possibles:
On peut gérer le mot réduit à l'aide d'une pile. Les opérations de réduction
consistent à supprimer des éléments dans celle-ci, les tests sur ce qui précède ou ce
qui suit se font très simplement en consultant les premiers symboles de la pile. On peut
construire aussi un arbre de syntaxe abstraite en utilisant une autre pile qui contient
cette fois des arbres (c'est à dire des pointeurs sur des n
uds). Les deux piles sont traitées en parallèle, la réduction par une règle a pour
effet sur la deuxième pile de construire un nouvel arbre dont les fils se trouvent en
tête de la pile, puis à remettre le résultat dans celle-ci.