Les systèmes de parenthèses





Next: Les expressions arithmétiques
Up: Exemples de Grammaires
Previous: Exemples de Grammaires
Le langage des systèmes de parenthèses joue un rôle important tant
du point de vue de la théorie des langages que de la programmation.
Dans les langages à structure de blocs, les begin end
ou les { } se comportent comme des parenthèses ouvrantes
et fermantes. Dans des langages comme Lisp, le décompte correct des
parenthèses fait partie de l'habileté du programmeur. Dans ce qui
suit, pour simplifier l'écriture, on note  une parenthèse
ouvrante et
une parenthèse
ouvrante et 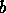 une parenthèse fermante. Un mot de
une parenthèse fermante. Un mot de 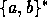 est
un système de parenthèses s'il contient autant de
est
un système de parenthèses s'il contient autant de  que de
que de 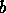 et
si tous ses facteurs gauches contiennent un nombre de
et
si tous ses facteurs gauches contiennent un nombre de  supérieur
ou égal au nombre de
supérieur
ou égal au nombre de 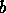 . Une autre définition possible est
récursive, un système de parenthèses
. Une autre définition possible est
récursive, un système de parenthèses 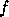 est ou bien le mot vide
est ou bien le mot vide 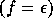 ou bien formé par deux systèmes de parenthèses
ou bien formé par deux systèmes de parenthèses
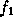 et
et 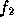 encadrés par
encadrés par  et
et 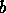 (
(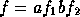 ). Cette
nouvelle définition se traduit immédiatement sous la forme de
la grammaire suivante:
). Cette
nouvelle définition se traduit immédiatement sous la forme de
la grammaire suivante:
 ,
, 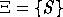 , l'axiome est
, l'axiome est 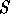 et les règles sont
données par:
et les règles sont
données par:
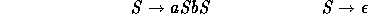
On notera la simplicité de cette grammaire, la définition
récursive rappelle celle des arbres binaires, un tel arbre est
construit à partir de deux autres comme un système de parenthèses
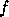 l'est à partir de
l'est à partir de 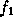 et
et 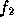 .
La grammaire précédente a la particularité, qui est parfois un
inconvénient, de contenir une règle dont le membre droit est le mot
vide. On peut alors utiliser une autre grammaire déduite de la
première qui engendre l'ensemble des systèmes de parenthèses non
réduits au mot vide, dont les règles sont:
.
La grammaire précédente a la particularité, qui est parfois un
inconvénient, de contenir une règle dont le membre droit est le mot
vide. On peut alors utiliser une autre grammaire déduite de la
première qui engendre l'ensemble des systèmes de parenthèses non
réduits au mot vide, dont les règles sont:
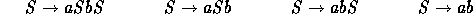
Cette transformation peut se généraliser et on peut ainsi
pour toute grammaire G trouver une grammaire qui engendre le
même langage, au mot vide près, et qui ne contient pas de règle de
la forme 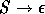 .
.





Next: Les expressions arithmétiques
Up: Exemples de Grammaires
Previous: Exemples de Grammaires

 ,
,