Le but de l'analyse syntaxique est d'abord déterminer si un mot appartient
ou non au langage engendré par une grammaire. Il s'agit donc, étant
donné un mot 
de construire la suite des dérivations qui a permis
de l'engendrer. Si l'on pratique ceci à la main pour de petits
exemples on peut utiliser la technique classique dite
``essais-erreurs'' consistant à tenter de deviner à partir d'un mot
la suite des dérivations qui ont permis de l'engendrer. Cette suite
se présente bien plus clairement sous forme d'un arbre, dit arbre de dérivation dont des exemples sont donnés figures
et . Il s'agit de ceux obtenus pour les
mots 
et 
engendrés respectivement
par la grammaire des systèmes de parenthèses et par celle des
expressions infixes. On verra que ces arbres, ou plutôt une version
plus compact de ceux-ci, jouent un rôle
important pour la phase suivante de la compilation.
Une définition rigoureuse et complète des arbres de
dérivation serait longue, contentons nous de quelques indications
informelles. Dans un tel arbre, les n
uds internes sont étiquetés
par des lettres auxiliaires (appartenant à 
) les feuilles par
des lettres de l'alphabet terminal. L'étiquette de la racine est
égale à l'axiome. Pour un n ud interne d' étiquette 
, le mot
obtenu en lisant de gauche à droite les étiquettes de ses fils
est tel que 
est une règle. Enfin, le mot dont on fait
l'analyse est constitué des étiquettes des feuilles lues de gauche
à droite.
Pour un mot donné du langage engendré par une grammaire,
l'arbre de dérivation n'est pas nécessairement unique. L'existence
de plusieurs arbres de dérivations pour un même programme signifie
en général qu'il existe plusieurs interprétations possibles pour
celui ci. On dit que la grammaire est ambiguë, c'est le cas pour
l'imbrication des if then et if then else en Pascal. Des
indications supplémentaires dans le manuel de référence du langage
permettent alors de lever l'ambiguïté et d'associer un arbre unique
à tout programme Pascal. Ceci permet de donner alors une
interprétation unique. Toutes les grammaires données plus haut sont
non-ambiguës, ceci peut se démontrer rigoureusement, toutefois les
preuves sont souvent techniques et ne présentent pas beaucoup
d'intérêt.
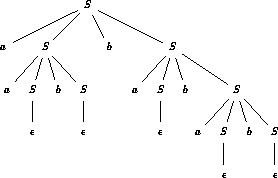
Figure: Arbre de dérivation de
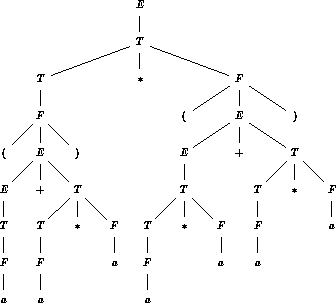
Figure: Arbre de dérivation d'une expression arithmétique
L'arbre de dérivation est parfois appelé arbre de syntaxe
concrète pour le distinguer de l'arbre de syntaxe abstraite
construit généralement par le compilateur d'un langage de
programmation. Cet arbre de syntaxe abstraite est plus compact que le
précédent et contient des informations sur la suite des actions
effectuées par un programme. Chaque n ud interne de cet arbre
possède une étiquette qui désigne une opération à exécuter. Il
s'obtient par des transformations simples à partir de l'arbre de
dérivation. On donne en exemple figure l'arbre de
syntaxe abstraite correspondant à l'arbre de dérivation de la figure
.
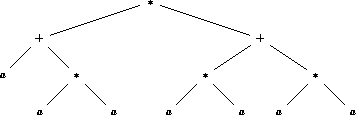
Figure: Arbre de syntaxe abstraite de l'expression