, 
,
l'axiome est 
.
Les règles sont données par :
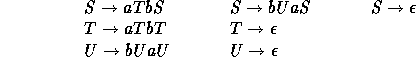
Pour engendrer des mots à l'aide d'une grammaire, on applique le procédé suivant:
On part de l'axiomeet on choisit une règle de la forme
. Si
ne contient aucune lettre auxiliaire, on a terminé. Sinon, on écrit
. On choisit une règle de la forme
. On remplace
. On répète l'opération sur
et ainsi de suite jusqu'à obtenir un mot qui ne contient que des lettres de
.
Dans la mesure où il y a plusieurs choix possibles à
chaque étape on voit que le nombre de mots engendrés par une
grammaire est souvent infini. Mais certaines grammaires peuvent
n'engendrer aucun mot. C'est le cas par exemple des grammaires dans
lesquelles tous les membres droits des règles contiennent un lettre
de 
.
On peut formaliser le procédé qui engendre les mots d'une
grammaire de façon un peu plus précise en définissant la notion
de dérivation. Etant donnés deux mots et 
contenant
des lettres de 
, on dit que u dérive
directement de v pour la grammaire 
, et on note 
,
s'il existe deux mots 
et 
et une règle de grammaire 
de tels que 
et 
. On dit
aussi que se dérive directement en .
On dit que dérive de , ou que se dérive
en , si s'obtient à partir de par une suite finie de
dérivations directes. On note alors:
Ce qui signifie l'existence de 
, , 
,
tels que 
, 
et pour tout 
, on a 
.
Un mot est engendré par une grammaire , s'il dérive de
l'axiome et ne contient que des lettres de , l'ensemble de tous les
mots engendrés par la grammaire , est le langage
engendré par ; il est noté 
.