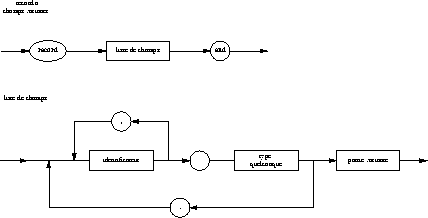
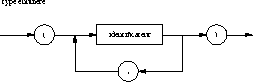
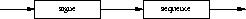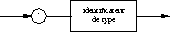Toute donnée manipulée par un programme PASCAL est typée. Le but
de ce chapitre est de décrire les types disponibles, á savoir :
Fonctions prédéfinies :
Si x est de type réel
abs : x abs(x) = |2| , la valeur absolue de x
sqr : x sqr(x) = x
sqrt : x sqrt(x) = x, la racine carrée positive de x, avec x>=0
sin : x sin(x), le sinus de x radians
cos : x cos(x), le cosinus de x radians
arctan : x arctan(x), l'arc tangente, en radians, de x
ln : x ln(x), avecx > 0
exp : x exp(x) = e
trunc : x trunc(x) = la partie entière de x ( x si x>0, et x si x > 0)
round : x round(x) = l'entier le plus proche de x (
trunc(x - 0.5) si x 0, trunc(x + 0.5) si x > 0 ).
Remarque : les fonctions pred, succ, ord ne sont pas
prédéfinies sur les réels.
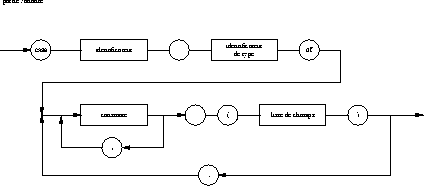
1.5. Types énumérés
- Ensemble des valeurs : l'ensemble des valeurs est défini par
extension.
- Littéraux : un type énuméré est défini en fournissant la
suite des valeurs qui le composent de la façon suivante :
type énuméré:
Un littéral du type ainsi défini est alors l'un des identificateurs
qui apparaissent dans la définition. Ces identificateurs
ne peuvent pas avoir été déclarés auparavant (dans une
déclaration de constante) et ne peuvent plus être utilisés
pour désigner des littéraux d'un autre type énuméré.
Attention ! En PASCAL, on n'utilise pas les accolades pour
définir l'ensemble des valeurs.
Exemples
(lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche)
(blanc, jaune, orange, rouge, vert, bleu, indigo)
Des exemples de littéraux sont les suivants :
mardi
jaune
bleu
samedi
- Ordre : l'ordre est l'ordre d'énumération dans la définition
du type.
Dans les exemples cidessus, on a donc :
lundi < mardi < mercredi < jeudi < vendredi < samedi < dimanche
blanc < jaune < orange < rouge < vert < bleu < indigo
- Opérateurs : tous les opérateurs relationnels
= < > <= >= <>
- Fonctions prédéfinies :
Si x est une valeur de type énuméré :
pred : x pred(x) = la valeur précédant x dans la liste d'énumération de la définition;
la fonction n'est pas définie pour le premier élément de la liste;
succ : x succ(x) = la valeur suivant x dans l'ordre d'énumération;
la fonction n'est pas définie pour le dernier élément de la liste;
ord : x ord(x) = la position de x dans la liste des valeurs énumérées
dans la définition; la première position est l'entier 0.
Exemples
succ(blanc) a pour valeur jaune
pred(samedi) a pour valeur vendredi
ord(mardi) a pour valeur 1, ord(blanc) a pour valeur 0,
ord(indigo) a pour valeur 6.
1.6. Types intervalles
- Ensemble des valeurs : il est défini par un intervalle de
valeurs prises dans un des types simples suivant :
integer, Boolean, char ou type énuméré.
Lorsqu'on définit un type intervalle, le type des éléments de
l'intervalle est appelé le type de base.
- Littéraux : un type intervalle est défini par la valeur minimale
et la valeur maximale de l'intervalle selon la syntaxe
suivante :
type intervalle:

où
- constante est
- soit un littéral,
- soit un identificateur de constante
(cfr Ch 3.1)
, précédé éventuellement du signe + ou -.
- constante1 constante2.
Un littéral de type intervalle est un des littéraux du type
de base dont la valeur est comprise entre la valeur minimale
et la valeur maximale de la définition (bornes comprises).
Avec les exemples précédents, on peut définir les types intervalles suivants :
mardi..vendredi
jaune..bleu
blanc..indigo
On peut aussi définir les types suivants :
1..10
'a'..'z'
- Ordre : celui du type de base.
- Opérateurs : ceux du type de base mais restreints á
l'intervalle.
- Fonctions prédéfinies : celles du type de base.
2. Types structurés
La section précédente montre qu'un type simple se définit entre
autres par un ensemble de valeurs et que chaque valeur de type
simple est un scalaire.
La valeur d'un type structuré, par contre, n'est pas un scalaire
: chaque valeur est ellemême une collection de valeurs.
L'objet de cette section est de présenter les différents types
structurés.
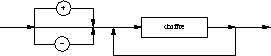
2.1. Tableaux (array of ...)
2.1.1. Définition et diagramme syntaxique
Un type tableau (array) est un type structuré permettant de
définir une collection finie et ordonnée de valeurs toutes de
même type. La collection est ordonnée : chaque valeur est
repérable par sa position au sein de la collection, position
identifiée par un ou plusieurs indices. Pour définir
complètement un type tableau, il faut spécifier
- le type des valeurs que doit contenir le tableau : c'est un
type quelconque;
- le type de chaque indice : ce ne peut être qu'un type
énuméré, un type intervalle, le type Boolean, le type char
ou tout type synonyme de ces types
(cfr Ch 4.3).
2.1.2. Strings
Le type
packed array [1..N] of char
(avec N une constante 1) définit un tableau de N caractères
encore appelé une chaîne de N caractères ou string.
Le mot packed signifie que la représentation en mémoire est
optimisée.
L'accès aux éléments est cependant moins efficace.
En fait, on peut définir n'importe quel type structuré comme étant
packed.
L'intérêt de cette technique est discutable sauf dans le cas présent.
Ces chaînes de caractères se manipulent comme les autres tableaux
(en particulier, on peut accéder á chacun des caractères qui les
composent). Mais contrairement aux autres tableaux, ces chaînes
possèdent les caractéristiques suivantes :
- Littéraux : Un littéral de type chaîne de caractères est une
suite de caractères, entourées d'apostrophes.
Exemples
'abcd'
'ceci est une chaine de caracteres de longueur superieure a 34'
' ' (chaîne vide)
'Braine l''Alleud' (on redouble l'apostrophe pour l'inclure dans une chaîne de caractères)
- Ordre : c'est l'ordre lexicographique basé sur l'ordre des
caractères. L'ordre n'est défini que pour des chaînes de
caractères de même longueur.
Exemples
'abcd' < 'abce' < 'acde' < 'bcde'
- Opérateurs : tous les opérateurs relationnels; les opérandes
doivent être des chaînes de caractères de même longueur.
- Fonctions prédéfinies : néant
- Remarque : en Turbo-PASCAL, il existe des types
structurés string qui sont une autre possibilité pour représenter
et manipuler des chaînes de caractères. Pour ces types lá, il existe
des fonctions et procédures prédédinies(
concaténation, par exemple )
2.1.3. Tableaux multidimensionnels
On appelle tableau multidimensionnel un tableau á plusieurs
indices.
Exemples
- array[1..M, 1..N] of integer définit une matrice M×N d'entiers (M
et N sont des constantes supposées définies auparavant).
- array[1..10, 5..20, 0..30] of real définit un tableau
tridimensionnel 10 × 16 × 31 de nombres réels.
Remarque
Un tableau multidimensionnel á k indices peut être vu comme un
tableau de tableaux de k-1 indices. Par exemple, une matrice M×N
peut être vue comme un vecteur de M valeurs, chaque valeur étant
ellemême un vecteur de N éléments.
Comme le type des valeurs d'un tableau en PASCAL peut être quelconque,
on peut définir les tableaux multidimensionnels comme des
tableaux de tableaux.
Exemples
Les deux tableaux définis cidessus auraient pu l'être comme suit :
- array[1..M] of array[1..N] of integer
- array[1..10] of array[5..20,0..30] of integer
- ou bien
array[1..10, 5..20] of array[0..30] of integer
- ou encore
array[1..10] of array[5..20] of array[0..30] of integer
Remarque
La déclaration
array [1..1000, 1..1000] of integer
définit une matrice d' un million de nombres entiers ! Beaucoup
d'ordinateurs imposent des limites quant au nombre total d'objets
représentables simultanément en mémoire (sans oublier que les
constructions d'un programme prennent également de la place !).
Un million de nombres entiers occupent une place qui dépasse
l'espace disponible dans un grand nombre d'ordinateurs de petite
ou moyenne taille.
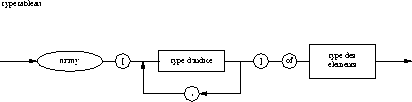
2.2. Enregistrements (record)
Un type record (on dit encore structure ou enregistrement) est un
type structuré permettant de définir une collection finie de
valeurs pouvant être de types différents. Chaque valeur est
appelé un champ de la structure. A chaque champ est associé un
nom; ce nom (ou identificateur) permet de désigner la valeur dans
les expressions
(cfr Ch 7).
Il est clair que tous
les champs d'une structure doivent avoir des noms différents.
Pour définir complètement un type record, il faut spécifier
- le nom de chaque champ;
- le type de chaque champ; c'est un type quelconque.
- Diagrammes syntaxiques :
type record :

liste de champs :
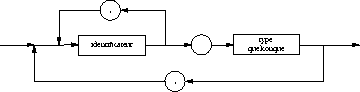
Exemples
record
jour,mois,annee : integer
end;
record
nom,prenom : packed array [1..20] of char;
noma : integer;
end;
record
annee : 1900..2000;
couleur : (rouge,brun,noir,bleu,blanc);
marque : packed array [1..20] of char
end;
- Littéraux : le langage PASCAL standard ne permet pas de
représenter une valeur de type record (c'estádire un enregistrement)
sous forme de littéral.
- Ordre : aucun ordre n'est défini sur les valeurs de type
record. On ne peut donc comparer deux enregistrements
comme, par exemple, on compare deux valeurs entières avec les
opérateurs relationnels.
- Opérateurs : néant.
- Fonctions standard : néant.
Cas particulier : les enregistrements á champs variants
On a vu dans le paragraphe précédent que pour définir
complètement un type record, il faut spécifier le nom de chaque
champ et le type de chaque champ.
Il existe des applications où la valeur d'un champ influence la
signification d'autres champs. Par exemple, supposons qu'une
administration communale belge souhaite répertorier ses
habitants; s'il s'agit de Belges, on souhaite connaître leur régime
linguistique; s'il s'agit d'étrangers, on souhaite connaître leur
nationalité.
Un record á champs variants permet de rendre l'existence d'un
champ dépendant de la valeur d'une autre champ de la structure.
On notera que la partie variante du record doit être la dernière
partie de la définition du record.
L'utilisation de ce type de record est expliqué en
Ch 8.2.4
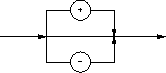
2.3. Ensembles (set of ...)
Le set correspond partiellement au concept mathémathique
d'ensemble, c'estádire une collection d'éléments tous du même
type, sans répétition. En PASCAL, le type des éléments contenus
dans l'ensemble doit être un type énuméré, un type intervalle, le
type Boolean ou le type char; ce type peut être donné
explicitement ou par un identificateur de type
(cfr Ch 4).
- Diagramme syntaxique
type set :
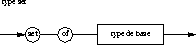
Exemples
set of 0..9
set of (lundi,mardi,mercredi,jeudi,vendredi,samedi,dimanche)
set of char
- Littéraux : un littéral de type set est une énumération
d'éléments notés entre crochets [ et ];
les éléments, tous de même type, sont séparés par des virgules:
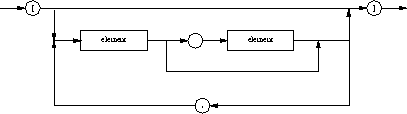
Exemples
[1,2,5,8]
[lundi..mercredi,dimanche]
[´0´..´9´,´a´..´z´,´A´..´Z´]
- Ordre : l'ordre défini sur les valeurs du type set est
l'inclusion. Ce n'est donc pas un ordre total.
- Opérateurs :
Les opérateurs binaires
+ : union
* : intersection
- : différence
sur deux opérandes (cfr Ch 7) de même type
set fournissent un résultat du même type.
Les opérateurs binaires
= : égalité
<> : inégalité
<= : inclusion du premier opérande dans le second opérande
>= : inclusion du second opérande dans le premier opérande
sur deux opérandes de même type set fournissent un
résultat booléen.
L'opérateur
in : appartenance d'un élément á un ensemble
fournit un résultat booléen (vrai si l'élément
appartient á l'ensemble).
- Fontions prédéfinies : néant.
- Restrictions : en pratique, les variables de type set sont
implémentées au moyen d'un nombre fini de bits. Les
opérateurs sur les ensembles sont alors implémentés par de
simples opérations sur les bits. Ceci a pour conséquence de
rendre ces opérations très efficaces mais aussi de limiter la
taille maximale admissible des ensembles. Dès lors, de nombreux
compilateurs PASCAL refusent les types "set of integer".
En particulier, le Turbo-PASCAL n'accepte pas d'ensembles de
plus de 256 éléments.
2.4. Fichiers (file of ...)
Un fichier est une collection totalement ordonnée (ou séquence)
d'éléments de même type. La longueur d'un fichier, définie par
le nombre d'éléments du fichier peut varier et n'est pas fixée
dans le type.
Cfr Ch 10
pour l'usage des objets de
type file of.
- Diagramme syntaxique
file of type

où type désigne un type quelconque á l'exception de
- file of ...
- un type ayant comme composante un "file of ..."
- Littéraux : néant.
- Ordre : néant.
- Opérateurs : néant.
- Procédures et fonctions prédéfinies :
- Procédures prédéfinies
reset read
rewrite write
- Fonctions prédéfinies
eof
- Cas particulier : type text
Le type text est prédéfini dans le langage.
Toutes les propriétés des fichiers s'appliquent au type text.
On a, en plus,
- les procédures prédéfinies
readln writeln
- la fonction prédéfinie
eoln
3.Types pointeurs
A tout identificateur de type T
(cfr Ch 4)
peut être
associé un type ``pointeur vers un élément de type T'', dont les
valeurs sont soit des ``adresses'' d'éléments de type T, soit une
valeur conventionnelle appelée valeurnil, et qui n'est l'adresse
d'aucun élément
(cfr Ch 9).